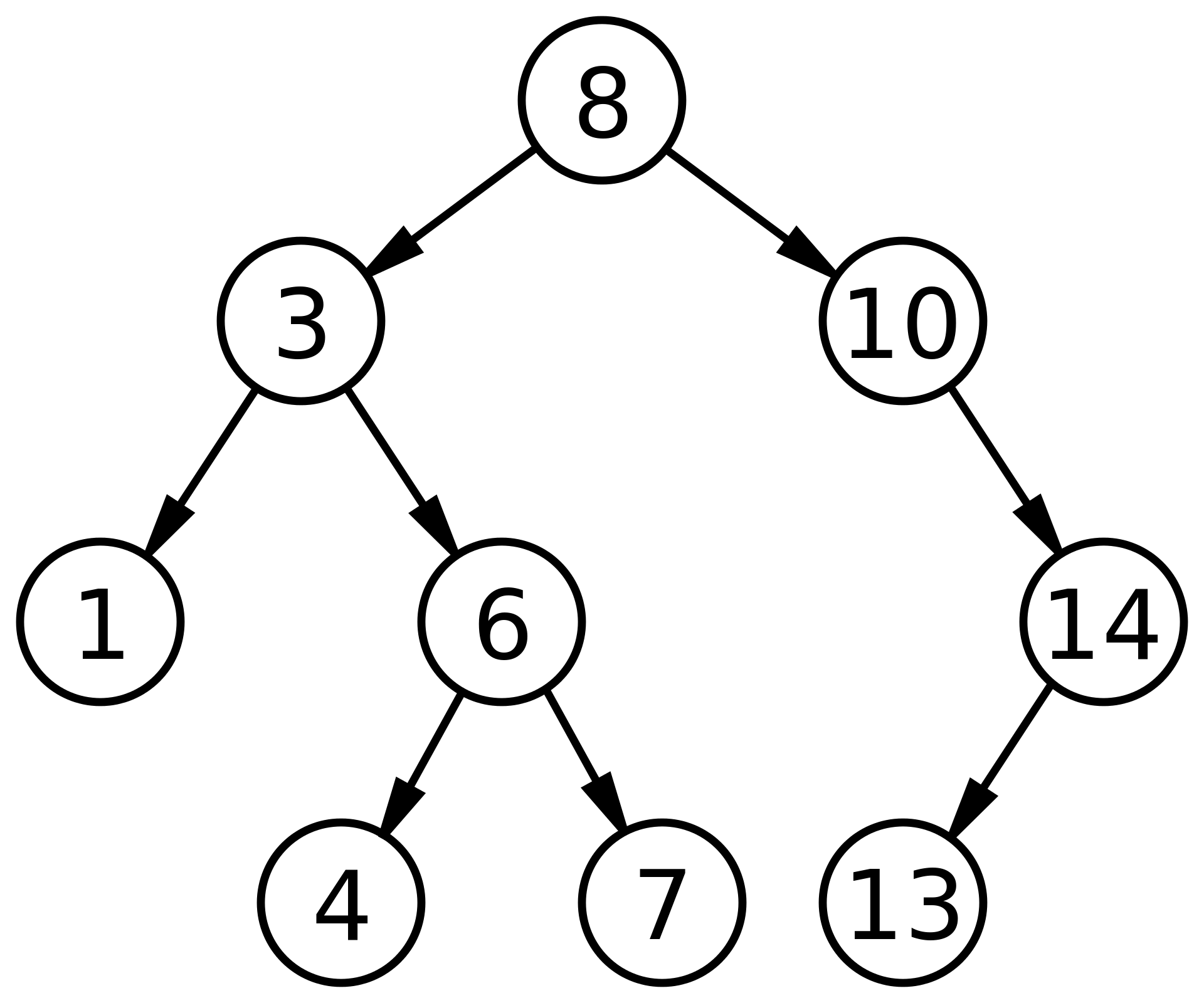
Trees

Trees are a non-linear data structure that allow us to implement a range of agorithms that are faster than using linear data structures like array-based lists or linked lists. Trees also provide a natural organizationof data, and have become ubiquitous structures in file systems, GUIs, databses etc.

Trees are hierarchical representation of a set of nodes storing elements such that the nodes have a parent-child relationship with the following definitions and properties:

• root - top node of a tree
• parent - except for the root node, all nodes in a tree have a parent
• children - nodes in a tree may have zero or more children
• depth \(d_p\) - for a position p of a node in a tree T, the depth of p is the number of ancestors of p, excluding p itself. (but it includes the root node)
• e.g. if p is the root, then its depth is 0, otherwise it is 1 + depth of the parent
• height \(h_p\) - defined from the leaf of the tree, defined recursively
• e.g. if p is the leaf of a tree, its height is 0, otherwise it is 1 + max(height of children)
• the height of a non-empty tree T is equal to the maximum of the depths of its leaf positions

In a tree, each node of the tree apart from the root node has a unique parent node, and every node with a parent is a child node.

Trees can be empty (i.e. don't even have a root node) which allows for recursive definitions such that:

1. a tree T is either empty or consists of a root node r
2. root node r has a set of set of subtrees whose roots are the children of r

Ordered Trees

A tree is ordered if there is a meaningful linear order among the children of each node - i.e. we can identify the children of a node as being the first, second, third and so on. This is usually visualized by arranng siblings left to right, according to their order.

Tree Abstract Base Class

from abc import ABC, abstractmethod

class Position(ABC):

    def element(self):
        raise NotImplementedError('must be implemented by subclass')

    def __eq__(self, other):
        raise NotImplementedError('must be implemented by subclass')

    def __ne__(self, other):
        return not self == other

class Tree(ABC):

    def root(self):
        raise NotImplementedError('must be implemented by subclass')

    def parent(self, position):
        raise NotImplementedError('must be implemented by subclass')

    def num_children(self, position):
        raise NotImplementedError('must be implemented by subclass')

    def children(self, position):
        raise NotImplementedError('must be implemented by subclass')

    def __len__(self):
        raise NotImplementedError('must be implemented by subclass')

    def is_root(self, position):
        return self.root() == position

    def is_leaf(self, position):
        return self.num_children(position) == 0

    def is_empty(self):
        return len(self) == 0

    def depth(self, position): # O(d_p + 1)
        if self.is_root(position):
            return 0
        else:
            return 1 + self.depth(self.parent(p))

    def _height(self, position): # O(n)
        if self.is_leaf(position):
            return 0
        else:
            return 1 + max(self.height(child) for child in self.children(position))

    def height(self, position=None):
        if not position:
            position = self.root()

        return self._height(position)

Linked Structure for General Trees

A natural way to represent a tree is through a linked structure, with nodes that maintain references to the elment stores at a position p and to the nodes associated with the children and parent of p.

For a general tree, there is no limit on the number of children that a node may have. A natural way to realize a general tree T as a linked structure is to have each node store a single container of references to its children.

The tree itself also maintainsan instance variable storing a reference to the root node, and a variable called size that represents the overall number of nodes of T.

class TreeNode:
    __slots__ = '_element', '_parent', '_left', '_right'

    def __init__(self, element, parent=None, children=[]):
        self._element = element
        self._parent = parent
        self._children = children

class TreePosition(Position):

    def __init__(self, container, node):
        self._container = container
        self._node = node

    def element(self):
        return self._node._element

    def __eq__(self, other):
        return type(other) is type(self) and other._node is self._node

class GeneralTree(Tree):

    def __init__(self):
        self._root = None
        self._size = 0

    def _make_position(self, node):
        return self.Position(self, node) ifnode is not None else None

    def _validate(self, p):
        if not isinstance(p, self.Position):
            raise TypeError('p must be proper Position type')

        if p._container is not self:
            raise ValueError('p does not belong to this container')

        if p._node._parent is p._node:
            raise ValueError('p is no longer valid')

        return p._node

    def __len__(self):
        return self._size

    def root(self):
        return self._make_postion(self._root)

    def parent(self, p):
        node = self._validate(p)
        return self._make_position(node._parent)

    def children(self, p):
        node = self._validate(p)
        return self._make_position(node._children)

    def num_children(self, p):
        node = self._validate(p)
        return len(node._children)

    def __iter__(self):
        for p in self.positions():
            yield p.element()

    def positions(self):
        return self.preorder()

    def preorder(self):
        if not self.is_empty():
            for p in self._subtree_preorder(self.root()):
                yield p

    def _subtree_preorder(self, p):
        yield p
        for c in self.children(p):
            for other in self._subtree_preorder(c):
                yield other

    def postorder(self):
        if not self.is_empty():
            for p in self._subtree_postorder(self.root()):
                yield p

    def _subtree_postorder(self, p):
        for c in self.children(p):
            for other in self._subtree_postorder(c):
                yield other
        yield p

    def breadthfirst(self):
        if not self.is_empty():
            fringe = LinkedQueue()
            fringe.enqueue(self.root())
            while not fringe.is_empty():
                p = fringe.dequeue()
                yield p
                for c in self.children(p):
                    fringe.enqueue(c)

Binary Trees

A binary tree is an ordered tree with the following properties:

1. Every node has at most two children
2. Each child node is labeled as being either a left child or a right child
3. A left child precedes a right child in the order of children of the node

The subtree rooted at the left child is called a left subtree and rooted at the right a right subtree.

Recursive Definitions of a Binary Search Tree

A binary tree is either empty or consists of:

1. a node r, called the root of T, that stores an element
2. a binary tree (possibly empty), called the left subtree of T
3. a binary tree (possibly empty), called the right subtree of T

Types

Proper/Full

A Full or Proper binary search tree is one where each node has either zero or two children. Therefore internal parent nodes always have exactly two children.

An example is expression trees that capture the arithmetic expression e.g. (((3+1)x3)/((9-5)+2) as shown below:

                (/)
                / \
               /   \
             (x)    (+)
            /  \    /  \
          (+)   3  (-)  2
         /  \      / \
        3    1    9   5

Perfect

All interior nodes have two children and all leaves have the same depth or same level. A perfect binary tree is also a full binary tree.

Complete

All levels of the binary tree (0, 1, 2, ..., h -1) have maximum number of nodes possible (i.e. \(2^i\) nodes for \(i \leq i \leq h-1\)) and the remaining nodes at level h reside in the leftmost possible positions at that level.

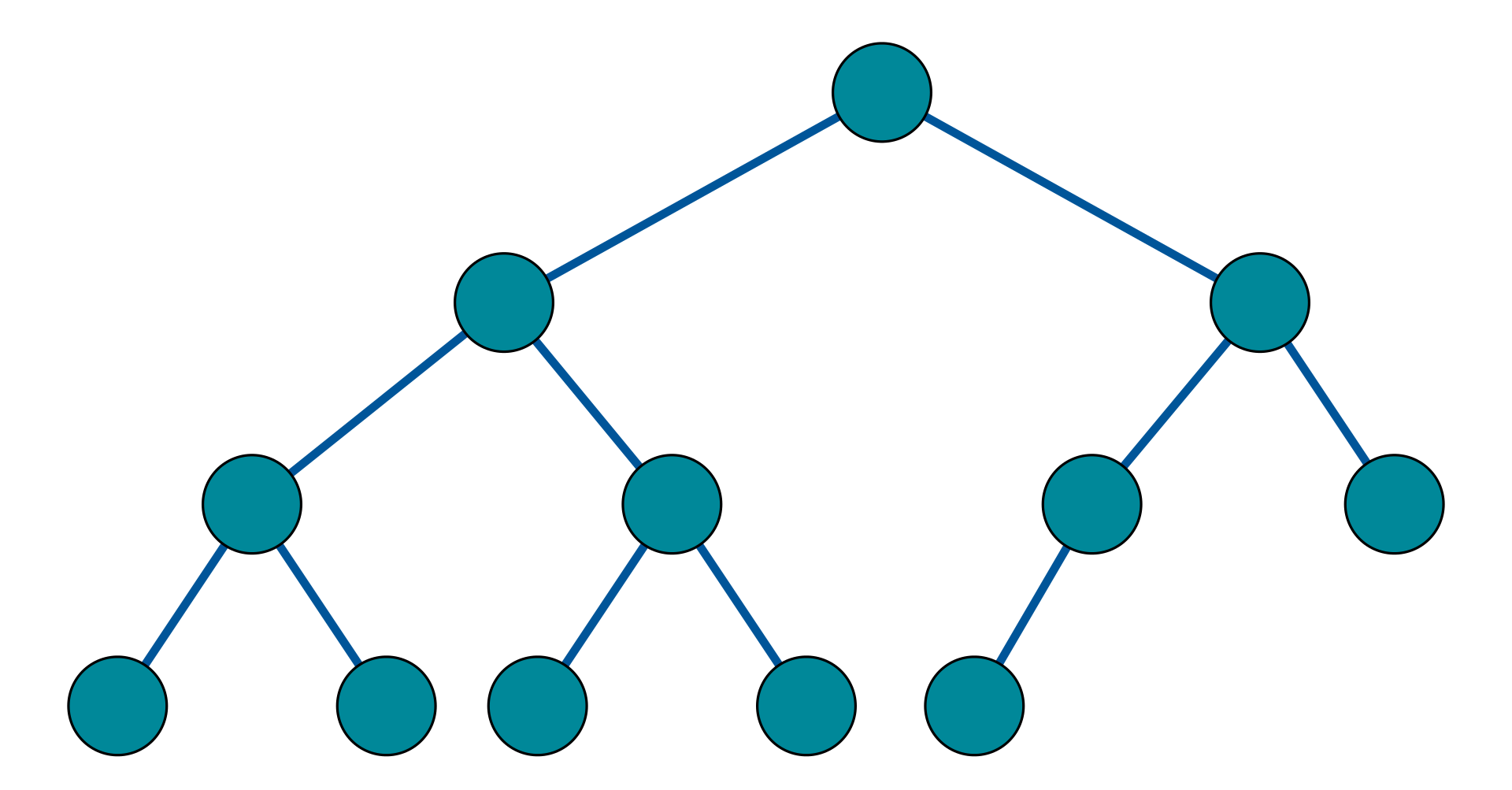
Balanced

Where left and rigt subtrees of every node differ in height by at most 1. i.e. where no leaf is much farther away from the root than any other leaf.

Properties

Level of a tree is a set of nodes at the same depth.

So in a binary tree, level 0 has at most 1 node. Level 1 has at most 2 nodes. Level 2 has at most 4 nodes etc.

So in general, a level d has at most \(2^d\) nodes.

Therefore from this we can see that the number of nodes at any given level is exponential. From this we can define the following properties where - \(n_E\) is number of external nodes, \(n_I\) is the number of internal nodes, \(n\) is the numberof nodes, and \(h\) is the height of the tree:

1. \(h + 1 \leq n \leq 2^{h+1}-1\)
2. \(1 \leq n_E \leq 2^h\)
3. \(h \leq n_I \leq 2^h - 1\)
4. \(log(n+1) - 1 \leq h \leq n - 1\)

Also if the tree is proper then:

1. \(2h + 1 \leq n \leq w^{h+1} - 1\)
2. \(h + 1 \leq n_E \leq 2^h\)
3. \(h \leq n_I \leq 2^h - 1\)
4. \(log(n+1) - 1 \leq h \leq (n-1)/2\)
5. \(n_E = n_I + 1\)

For reference, \(n_E\) = external nodes = nodes with no children. \(n_I\) = internal nodes = nodes which are not leaves.

Array Based Binary Tree

                (/)
                / \
               /   \
             (x)    (+)
            /  \    /  \
          (+)   3  (-)  2
         /  \      / \
        3    1    9   5

bfs: [/, x, +, +, 3, -, 2, 3, 1, 9, 5, Null, Null]
pre-order: [/, x, +, 3, Null, Null, 1, Null, Null, 3, Null, Null, +, -, 9, Null, Null, 5, Null, Null, 2, Null, Null]

BFS or level numbering of positions to build an array is fairly common. Here a position can be represented by a single integer - the main advantage of this data structure. But operations like deleting and promoting children takes O(n) time.

Utilizing the General Tree Linked Structure

For a binary tree the children are defined as left and right child.

class BinaryTreeNode:
    __slots__ = '_element', '_parent', '_left', '_right'

    def __init__(self, element, parent=None, left=None, right=None):
        self._element = element
        self._parent = parent
        self._left = left
        self._right = right

class BinaryTreePosition(Position):

    def __init__(self, container, node):
        self._container = container
        self._node = node

    def element(self):
        return self._node._element

    def __eq__(self, other):
        return type(other) is type(self) and other._node is self._node

class BinaryTree(Tree):

    def __init__(self):
        self._root = None
        self._size = 0

    def _make_position(self, node):
        return self.Position(self, node) ifnode is not None else None

    def _validate(self, p):
        if not isinstance(p, self.Position):
            raise TypeError('p must be proper Position type')

        if p._container is not self:
            raise ValueError('p does not belong to this container')

        if p._node._parent is p._node:
            raise ValueError('p is no longer valid')

        return p._node

    def __len__(self):
        return self._size

    def root(self):
        return self._make_postion(self._root)

    def parent(self, p):
        node = self._validate(p)
        return self._make_position(node._parent)

    def left(self, p):
        node = self._validate(p)
        return self._make_position(node._left)

    def right(self, p):
        node = self._validate(p)
        return self._make_position(node._right)

    def num_children(self, p):
        node = self._validate(p)
        count = 0:
        if node._left is not None:
            count += 1
        if node._right is not None:
            count += 1
        return len(count)

    def _add_root(self, e):
        if self._root is not None: raise ValueError('root exists')
        self._size = 1
        self._root = Node(e)
        return self._make_position(self._root)

    def _add_left(self, p, e):
        node = self._validate(p)
        if node._left is not None:
            raise ValueError('Left child exists')
        self._size += 1
        node._left = self._Node(e, node)
        return self._make_position(node._left)

    def _add_right(self, p, e):
        node = self._validate(p)
        if node._right is not None:
            raise ValueError('Right child exists')
        self._size += 1
        node._right = self._Node(e, node)
        return self._make_position(node._right)

    def _replace(self, p, e):
        node = self._validate(p)
        old = node._element
        node._element = e
        return old

    def _delete(self, p):
        node = self._validate(p)
        if self.num_children(p) == 2:
            raise ValueError('Position has two children')
        child = node._left if node._left else node._right
        if child is not None:
            child._parent = node._parent
        if node is self._root:
            self._root = child
        else:
            parent = node._parent
            if node is parent._left:
                parent._left = child
            else:
                parent._right = child
        self._size -= 1
        node._parent = node
        return node._element

    def _attach(self, p, t1, t2):
        node = self._validate(p)
        if not self.is_leaf(p):
            raise ValueError('position must be leaf')
        if not type(self) is type(t1) is type(t2):
            raise TypeError('Tree types must match')
        self._size += len(t1) + len(t2)
        if not t1.is_empty():
            t1._root._parent = node
            node._left = t1._root
            t1._root = None
            t1._size = 0
        if not t2.is_empty():
            t2._root._parent = node
            node._right = t2._root
            t2._root = None
            t2._size = 0

Tree Traversal Algorithms

Go to Algorithms >> Tree Traversals

We can also modify our base Tree class to implement the traversal methods as well, with the pre-order traversal being the default one.

Refer to Tree Abstract Base Class for the other parts of the base class.

Some key observations:

1. we implement the traversals as generator functions where we yield each position to the caller and let the caller decide what action to perform at that position
2. the positions method returns the iteration as an object - again acting as a generator
3. the breadth first search or bfs traversal is iterative - not recursive
4. the inorder traversal is only implemented for binary trees - it does not generalize for generic trees

class Tree(ABC):

    ...
    def positions(self):
        self.preorder()

    def preorder(self):
        if not self.is_empty():
            for p in self._subtree_preorder(self.root()):
                yield p

    def _subtree_preorder(self, p):
        yield p
        for c in self.children(p):
            for other in self._subtree_preorder(c):
                yield other

    def postorder(self):
        if not self.is_empty():
            for p in self._subtree_postorder(self.root()):
                yield p

    def _subtree_postorder(self, p):
        for c in self.children(p):
            for other in self._subtree_postorder(c):
                yield other
        yield p 

    def bfs(self):
        if not self.is_empty():
            fringe = LinkedQueue()
            fringe.enqueue(self.root())
            while not fringe.is_empty():
                p = fringe.dequeue()
                yield p
                for c in self.children(p):
                    fringe.enqueue(c)

    def inorder(self):
        if not self.is_empty():
            for p in self._subtree_inorder(self.root()):
                yield p

    def _subtree_inorder(self, p):
        if self.left(p) is not None:
            for other in self._subtree_inorder(self.left(p)):
                yield other
        yield p
        if self.right(p) is not None:
            for other in self._subtree_inorder(self.right(p)):
                yield other
    ...

As can be seen, while we can implement specific traversals for the Tree class, or the inorder method for binary trees, the code is not general enough to capture the range of computations possible. These were all custom implementations with some repeating algorithmic patterns (e.g. blending of work performed before or after recursion of subtrees).

A more general framework for implemting tree traversals is through Euler tour traversals which also uses the Template method.

Binary Search Trees

If we have a set of unique elements that have an order relation (e.g. a set of integers), we can construct a binary search tree such that for each position p of the tree T:

1. Position p stores an element of the set, denoted as e(p)
2. Elements stored in the left subtree of p (if any) are less than e(p)
3. Elements stored in the right subtree of p (if any) are greater than e(p)

Binary Search Trees can be used to efficiently implement a sorted map - assuming we have an order relation defined on the keys.

Navigating Binary Search Trees

An inorder traversal of a binary search tree visits positions in increasing order of their keys. Therefore if presented with a binary search tree, we can produce a sorted iteration of the keys of a map in linear time.

Hence binary search trees provide a way to produce ordered data in linear time.

Additionally binary search trees can be used to find:

1. position containing the greatest key that is less than the position p - the position that would be visited immediately before position p in an inorder traversal
2. position containing the least key that is great than the position p - the position that would be visited immediately after position p in an inorder traversal

def after(p):
    if right(p) is not None then {successor is leftmost position in p's right subtree}:
        walk = right(p)
        while left(walk) is not None do:
            walk = left(walk)
        return walk

    else: {successor is nearest ancestor having p in its left subtree}
        walk = p
        ancestor = parent(walk)
        while ancestor is not None and walk == right (ancestor) do:
            walk = ancestor
            ancestor = parent(walk)
        return ancestor

Searches

We can traverse a binary search tree to search for specific keys in O(log(n)) time complexty as long as it is balanced. In the worst (imbalanced) case the height h of the tree can be equal to the n in which case the time complexity would be O(h) = O(n) instead.

def TreeSearch(T, p, k):
    if k == p.key() then:
        return p
    else if k < p.key() and T.left(p) is not None then:
        return TreeSearch(T, T.left(p), k)
    else if k > p.key() and T.right(p) is not None then:
        return TreeSearch(T, T.right(p), k)
    return p # return the last node if key not found

Insertions

Search for key k, and if found, that item's existing value is reassigned. If not found, a new item is inserted into the underlying tree T in place of theempty subtree that was reached at the end of the fialed search.

def TreeInsert(T, k, v):
    # Tree T, search key k, and value v to be associated with key k
    p = TreeSearch(T, T.root(), k)
    if k == p.key() then:
        set p's value to v
    elif k < p.key() then:
        add node with item (k, v) as left child of p
    else:
        add node with item (k, v) as righ child of p

This is always enacted at the bottom of a path.

O(h)

Deletions

More complicated than insertions as they can happen in any part of the tree.

Steps: - If key k is successfully found in tree T: - if p has at most one child, delete item with key k at position p, and reoplace it with its child - if p has two children: locate the predecessor (the rightmost position of the left subtree of p) i.e. r = before(p), then use r as replace for the position p, and then delete r (simple as it does not have a right child by defition)

O(h)

Python Implementation

class BinarySearchTreePosition(BinaryTreePosition):
    def key(self):
      """Return key of map's key-value pair."""
      return self.element()._key

    def value(self):
      """Return value of map's key-value pair."""
      return self.element()._value

class BinarySearchTree(BinaryTree, MapBase):
    def _subtree_search(self, p, k):
        """Return Position of p's subtree having key k, or last node searched."""
        if k == p.key():                                   # found match
        return p                                         
        elif k < p.key():                                  # search left subtree
        if self.left(p) is not None:
            return self._subtree_search(self.left(p), k)   
        else:                                              # search right subtree
        if self.right(p) is not None:
            return self._subtree_search(self.right(p), k)
        return p                                           # unsucessful search

    def _subtree_first_position(self, p):
        """Return Position of first item in subtree rooted at p."""
        walk = p
        while self.left(walk) is not None:                 # keep walking left
        walk = self.left(walk)
        return walk

    def _subtree_last_position(self, p):
        """Return Position of last item in subtree rooted at p."""
        walk = p
        while self.right(walk) is not None:                # keep walking right
        walk = self.right(walk)
        return walk

    #--------------------- public methods providing "positional" support ---------------------
    def first(self):
        """Return the first Position in the tree (or None if empty)."""
        return self._subtree_first_position(self.root()) if len(self) > 0 else None

    def last(self):
        """Return the last Position in the tree (or None if empty)."""
        return self._subtree_last_position(self.root()) if len(self) > 0 else None

    def before(self, p):
        """Return the Position just before p in the natural order.

        Return None if p is the first position.
        """
        self._validate(p)                            # inherited from LinkedBinaryTree
        if self.left(p):
        return self._subtree_last_position(self.left(p))
        else:
        # walk upward
        walk = p
        above = self.parent(walk)
        while above is not None and walk == self.left(above):
            walk = above
            above = self.parent(walk)
        return above

    def after(self, p):
        """Return the Position just after p in the natural order.

        Return None if p is the last position.
        """
        self._validate(p)                            # inherited from LinkedBinaryTree
        if self.right(p):
        return self._subtree_first_position(self.right(p))
        else:
        walk = p
        above = self.parent(walk)
        while above is not None and walk == self.right(above):
            walk = above
            above = self.parent(walk)
        return above

    def find_position(self, k):
        """Return position with key k, or else neighbor (or None if empty)."""
        if self.is_empty():
        return None
        else:
        p = self._subtree_search(self.root(), k)
        self._rebalance_access(p)                  # hook for balanced tree subclasses
        return p

    def delete(self, p):
        """Remove the item at given Position."""
        self._validate(p)                            # inherited from LinkedBinaryTree
        if self.left(p) and self.right(p):           # p has two children
        replacement = self._subtree_last_position(self.left(p))
        self._replace(p, replacement.element())    # from LinkedBinaryTree
        p =  replacement
        # now p has at most one child
        parent = self.parent(p)
        self._delete(p)                              # inherited from LinkedBinaryTree
        self._rebalance_delete(parent)               # if root deleted, parent is None

    #--------------------- public methods for (standard) map interface ---------------------
    def __getitem__(self, k):
        """Return value associated with key k (raise KeyError if not found)."""
        if self.is_empty():
        raise KeyError('Key Error: ' + repr(k))
        else:
        p = self._subtree_search(self.root(), k)
        self._rebalance_access(p)                  # hook for balanced tree subclasses
        if k != p.key():
            raise KeyError('Key Error: ' + repr(k))
        return p.value()

    def __setitem__(self, k, v):
        """Assign value v to key k, overwriting existing value if present."""
        if self.is_empty():
        leaf = self._add_root(self._Item(k,v))     # from LinkedBinaryTree
        else:
        p = self._subtree_search(self.root(), k)
        if p.key() == k:
            p.element()._value = v                   # replace existing item's value
            self._rebalance_access(p)                # hook for balanced tree subclasses
            return
        else:
            item = self._Item(k,v)
            if p.key() < k:
            leaf = self._add_right(p, item)        # inherited from LinkedBinaryTree
            else:
            leaf = self._add_left(p, item)         # inherited from LinkedBinaryTree
        self._rebalance_insert(leaf)                 # hook for balanced tree subclasses

    def __delitem__(self, k):
        """Remove item associated with key k (raise KeyError if not found)."""
        if not self.is_empty():
        p = self._subtree_search(self.root(), k)
        if k == p.key():
            self.delete(p)                           # rely on positional version
            return                                   # successful deletion complete
        self._rebalance_access(p)                  # hook for balanced tree subclasses
        raise KeyError('Key Error: ' + repr(k))

    def __iter__(self):
        """Generate an iteration of all keys in the map in order."""
        p = self.first()
        while p is not None:
        yield p.key()
        p = self.after(p)

    #--------------------- public methods for sorted map interface ---------------------
    def __reversed__(self):
        """Generate an iteration of all keys in the map in reverse order."""
        p = self.last()
        while p is not None:
        yield p.key()
        p = self.before(p)

    def find_min(self):
        """Return (key,value) pair with minimum key (or None if empty)."""
        if self.is_empty():
        return None
        else:
        p = self.first()
        return (p.key(), p.value())

    def find_max(self):
        """Return (key,value) pair with maximum key (or None if empty)."""
        if self.is_empty():
        return None
        else:
        p = self.last()
        return (p.key(), p.value())

    def find_le(self, k):
        """Return (key,value) pair with greatest key less than or equal to k.

        Return None if there does not exist such a key.
        """
        if self.is_empty():
        return None
        else:
        p = self.find_position(k)
        if k < p.key():
            p = self.before(p)
        return (p.key(), p.value()) if p is not None else None

    def find_lt(self, k):
        """Return (key,value) pair with greatest key strictly less than k.

        Return None if there does not exist such a key.
        """
        if self.is_empty():
        return None
        else:
        p = self.find_position(k)
        if not p.key() < k:
            p = self.before(p)
        return (p.key(), p.value()) if p is not None else None

    def find_ge(self, k):
        """Return (key,value) pair with least key greater than or equal to k.

        Return None if there does not exist such a key.
        """
        if self.is_empty():
        return None
        else:
        p = self.find_position(k)                   # may not find exact match
        if p.key() < k:                             # p's key is too small
            p = self.after(p)
        return (p.key(), p.value()) if p is not None else None

    def find_gt(self, k):
        """Return (key,value) pair with least key strictly greater than k.

        Return None if there does not exist such a key.
        """
        if self.is_empty():
        return None
        else:
        p = self.find_position(k)
        if not k < p.key():                   
            p = self.after(p)
        return (p.key(), p.value()) if p is not None else None

    def find_range(self, start, stop):
        """Iterate all (key,value) pairs such that start <= key < stop.

        If start is None, iteration begins with minimum key of map.
        If stop is None, iteration continues through the maximum key of map.
        """
        if not self.is_empty():
        if start is None:
            p = self.first()
        else:
            # we initialize p with logic similar to find_ge
            p = self.find_position(start)
            if p.key() < start:
            p = self.after(p)
        while p is not None and (stop is None or p.key() < stop):
            yield (p.key(), p.value())
            p = self.after(p)

    #--------------------- hooks used by subclasses to balance a tree ---------------------
    def _rebalance_insert(self, p):
        """Call to indicate that position p is newly added."""
        pass

    def _rebalance_delete(self, p):
        """Call to indicate that a child of p has been removed."""
        pass

    def _rebalance_access(self, p):
        """Call to indicate that position p was recently accessed."""
        pass

    #--------------------- nonpublic methods to support tree balancing ---------------------

    def _relink(self, parent, child, make_left_child):
        """Relink parent node with child node (we allow child to be None)."""
        if make_left_child:                           # make it a left child
        parent._left = child
        else:                                         # make it a right child
        parent._right = child
        if child is not None:                         # make child point to parent
        child._parent = parent

    def _rotate(self, p):
        """Rotate Position p above its parent.

        Switches between these configurations, depending on whether p==a or p==b.

            b                  a
            / \                /  \
            a  t2             t0   b
        / \                     / \
        t0  t1                  t1  t2

        Caller should ensure that p is not the root.
        """
        """Rotate Position p above its parent."""
        x = p._node
        y = x._parent                                 # we assume this exists
        z = y._parent                                 # grandparent (possibly None)
        if z is None:            
        self._root = x                              # x becomes root
        x._parent = None        
        else:
        self._relink(z, x, y == z._left)            # x becomes a direct child of z
        # now rotate x and y, including transfer of middle subtree
        if x == y._left:
        self._relink(y, x._right, True)             # x._right becomes left child of y
        self._relink(x, y, False)                   # y becomes right child of x
        else:
        self._relink(y, x._left, False)             # x._left becomes right child of y
        self._relink(x, y, True)                    # y becomes left child of x

    def _restructure(self, x):
        """Perform a trinode restructure among Position x, its parent, and its grandparent.

        Return the Position that becomes root of the restructured subtree.

        Assumes the nodes are in one of the following configurations:

            z=a                 z=c           z=a               z=c  
        /  \                /  \          /  \              /  \  
        t0  y=b             y=b  t3       t0   y=c          y=a  t3 
            /  \            /  \               /  \         /  \     
            t1  x=c         x=a  t2            x=b  t3      t0   x=b    
            /  \        /  \               /  \              /  \    
            t2  t3      t0  t1             t1  t2            t1  t2   

        The subtree will be restructured so that the node with key b becomes its root.

                b
                /   \
            a       c
            / \     / \
            t0  t1  t2  t3

        Caller should ensure that x has a grandparent.
        """
        """Perform trinode restructure of Position x with parent/grandparent."""
        y = self.parent(x)
        z = self.parent(y)
        if (x == self.right(y)) == (y == self.right(z)):  # matching alignments
        self._rotate(y)                                 # single rotation (of y)
        return y                                        # y is new subtree root
        else:                                             # opposite alignments
        self._rotate(x)                                 # double rotation (of x)     
        self._rotate(x)
        return x                                        # x is new subtree root

Self Balancing Trees

Some sequences of operations on binary search trees may lead to an unbalanced tree with height proportional to n. Hence we may only claim O(n) search.

However there are common search tree algorthms that provide stronger performance guarantees. AVL, Splay and Red-Black trees are based on augmenting the standard binary search tree with occasional operations to reshape the tree and reduce its height.

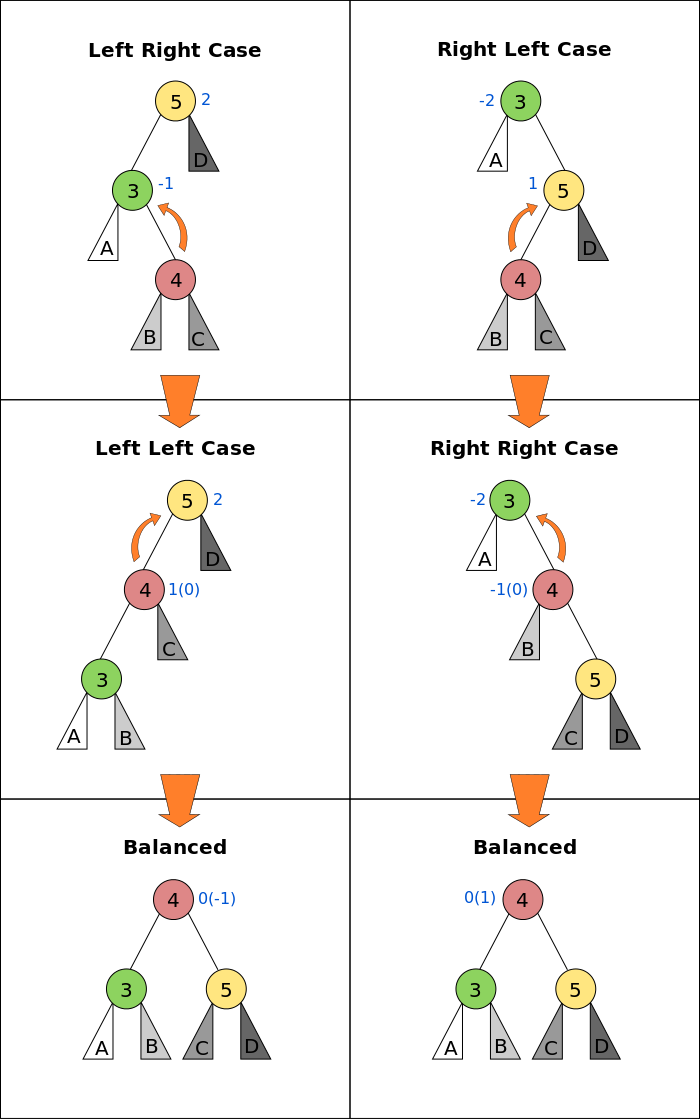
The primary operation to rebalance a binary search tree is known as a rotation. During a rotation, we "rotate" a child to be above its parent, as diagrammed below:

There are two primary types of rotations: left rotations and right rotations. Both types are used to adjust the structure of the tree without violating the binary search tree properties, where the left child of a node is less than the node, and the right child is greater.

Right Rotation

A right rotation is performed on a node that has a left child. This operation shifts the node down to the right, making its left child the new parent of the subtree. Here's how it works:

1. Given a node X with a left child Y, Y will become the new root of the subtree.
2. X's left subtree becomes Y's right subtree.
3. Y takes the place of X, and X becomes the right child of Y.

This operation is used when the tree becomes left-heavy, and we need to decrease the height of the left subtree to maintain balance.

Left Rotation

A left rotation is the mirror operation of a right rotation. It is performed on a node that has a right child, shifting the node down to the left and making its right child the new parent of the subtree. Here's the step-by-step process:

1. Given a node X with a right child Y, Y will become the new root of the subtree.
2. X's right subtree becomes Y's left subtree.
3. Y takes the place of X, and X becomes the left child of Y.

This operation is used when the tree becomes right-heavy, and we need to decrease the height of the right subtree.

Visual Representation

Let's illustrate both rotations with diagrams. For a right rotation:

    X               Y
   / \             / \
  Y   C   --->    A   X
 / \                 / \
A   B               B   C

class TreeNode:
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None

def rightRotate(root):
    newRoot = root.left
    root.left = newRoot.right
    newRoot.right = root
    return newRoot

and for a left rotation:

  X               Y
 / \             / \
A   Y    --->   X   C
   / \         / \
  B   C       A   B

def leftRotate(root):
    newRoot = root.right
    root.right = newRoot.left
    newRoot.left = root
    return newRoot

AVL Trees

AVL Trees store a balance factor on each node that follows the height balance property where for each position p of T, th heights of the children of p differ at most by 1.

The height is defined as the longest path from the node to a leaf.

Hence the subtree of an AVL tree is itself an AVL tree. The height of an AVL tree storing n entries is O(logn).

The insertion and deletion operations of AVL trees begin similarly to the corresponding operations for binary search trees, but with post-processing for each oepration to restore the balance of ay portions of the tree that are adversely affected by the change.

Insertion in AVL Trees

Insertion into an AVL tree involves several steps:

1. BST Insertion: The node is inserted following the binary search tree rules.
2. Updating Heights: After insertion, the heights of the ancestors of the inserted node are updated.
3. Balancing the Tree: If any ancestor node becomes unbalanced (balance factor is not -1, 0, or 1), rotations are performed to balance the tree.

Rotations for Rebalancing

Depending on the structure of the tree at the unbalanced node, one of the following rotations is performed:

• Single Right Rotation (LL Rotation): When the left subtree of the left child is causing the imbalance.
• Single Left Rotation (RR Rotation): When the right subtree of the right child is causing the imbalance.
• Left-Right Rotation (LR Rotation): When the right subtree of the left child is causing the imbalance.
• Right-Left Rotation (RL Rotation): When the left subtree of the right child is causing the imbalance.

Deletion in AVL Trees

Deletion from an AVL tree is a bit more complex:

1. Node Removal: Follows the basic BST deletion rules.
2. Balancing the Tree: After deletion, the tree might become unbalanced. The same procedure of updating heights and performing rotations is followed to restore balance.

Performance of AVL Trees

• Search: \(O(\log n)\) - AVL trees ensure that the height of the tree is always logarithmic in the number of nodes, guaranteeing efficient searches.
• Insertion: \(O(\log n)\) - Insertions may require a constant number of rotations, but the overall time complexity remains logarithmic.
• Deletion: \(O(\log n)\) - Similar to insertion, deletions are logarithmic in time complexity, including potential rotations for rebalancing.

Red-Black Trees

A Red-Black tree is characterized by several key properties:

1. Node Color: Each node is colored either red or black.
2. Root Property: The root node is always black.
3. Red Node Property: Red nodes cannot have red children. This means no two red nodes can be adjacent.
4. Black Height Property: Every path from a node to its descendant NULL nodes must contain the same number of black nodes. This consistent count of black nodes is known as the black height.
5. New Nodes are Red: Newly inserted nodes are always colored red. This helps maintain the black height property with fewer rotations.

Insertion

Inserting a new node into a Red-Black tree involves several steps:

1. BST Insertion: Initially, the node is inserted according to the rules of a binary search tree (BST), based on key comparisons.
2. Coloring: The new node is colored red.
3. Rebalancing: The tree is adjusted to maintain the Red-Black properties through recoloring and rotations.

The rebalancing phase takes into account various cases depending on the color of the uncle node (the sibling of the new node's parent) and the structure of the tree, aiming to fix any violations of the Red-Black properties.

Deletion

Deletion in a Red-Black tree is more complex due to the balancing properties:

1. Node Removal: Follows the BST deletion rules. If the node to be deleted has two children, it's replaced with its in-order successor or predecessor, which is then deleted.
2. Rebalancing: If a black node was deleted or replaced, the tree might need to be rebalanced to maintain the black height.

Rebalancing after deletion also considers several cases, focusing on the color of the sibling of the node being fixed and the color of the sibling's children.

Rotations

Rotations help maintain or restore Red-Black properties during insertions and deletions:

• Left Rotation: Performed when the tree is too heavy on the right, rotating a parent node to the left around its right child.
• Right Rotation: Used when the tree is too heavy on the left, rotating a parent node to the right around its left child.

Performance

Operations such as search, insertion, and deletion in Red-Black trees have a time complexity of \(O(\log n)\), where \(n\) is the number of nodes. This efficiency is due to the tree's self-balancing nature, ensuring operations remain fast.

Python Implementation

class RedBlackTreeMap(BinarySearchTree):
  """Sorted map implementation using a red-black tree."""

  #-------------------------- nested _Node class --------------------------
  class _Node(TreeMap._Node):
    """Node class for red-black tree maintains bit that denotes color."""
    __slots__ = '_red'     # add additional data member to the Node class

    def __init__(self, element, parent=None, left=None, right=None):
      super().__init__(element, parent, left, right)
      self._red = True     # new node red by default

  #------------------------- positional-based utility methods -------------------------
  # we consider a nonexistent child to be trivially black
  def _set_red(self, p): p._node._red = True
  def _set_black(self, p): p._node._red = False
  def _set_color(self, p, make_red): p._node._red = make_red
  def _is_red(self, p): return p is not None and p._node._red
  def _is_red_leaf(self, p): return self._is_red(p) and self.is_leaf(p)

  def _get_red_child(self, p):
    """Return a red child of p (or None if no such child)."""
    for child in (self.left(p), self.right(p)):
      if self._is_red(child):
        return child
    return None

  #------------------------- support for insertions -------------------------
  def _rebalance_insert(self, p):
    self._resolve_red(p)                         # new node is always red

  def _resolve_red(self, p):
    if self.is_root(p):
      self._set_black(p)                         # make root black
    else:
      parent = self.parent(p)
      if self._is_red(parent):                   # double red problem
        uncle = self.sibling(parent)
        if not self._is_red(uncle):              # Case 1: misshapen 4-node
          middle = self._restructure(p)          # do trinode restructuring
          self._set_black(middle)                # and then fix colors
          self._set_red(self.left(middle))
          self._set_red(self.right(middle))
        else:                                    # Case 2: overfull 5-node
          grand = self.parent(parent)            
          self._set_red(grand)                   # grandparent becomes red
          self._set_black(self.left(grand))      # its children become black
          self._set_black(self.right(grand))
          self._resolve_red(grand)               # recur at red grandparent

  #------------------------- support for deletions -------------------------
  def _rebalance_delete(self, p):
    if len(self) == 1:                                     
      self._set_black(self.root())  # special case: ensure that root is black
    elif p is not None:
      n = self.num_children(p)
      if n == 1:                    # deficit exists unless child is a red leaf
        c = next(self.children(p))
        if not self._is_red_leaf(c):
          self._fix_deficit(p, c)
      elif n == 2:                  # removed black node with red child
        if self._is_red_leaf(self.left(p)):
          self._set_black(self.left(p))
        else:
          self._set_black(self.right(p))

  def _fix_deficit(self, z, y):
    """Resolve black deficit at z, where y is the root of z's heavier subtree."""
    if not self._is_red(y): # y is black; will apply Case 1 or 2
      x = self._get_red_child(y)
      if x is not None: # Case 1: y is black and has red child x; do "transfer"
        old_color = self._is_red(z)
        middle = self._restructure(x)
        self._set_color(middle, old_color)   # middle gets old color of z
        self._set_black(self.left(middle))   # children become black
        self._set_black(self.right(middle))
      else: # Case 2: y is black, but no red children; recolor as "fusion"
        self._set_red(y)
        if self._is_red(z):
          self._set_black(z)                 # this resolves the problem
        elif not self.is_root(z):
          self._fix_deficit(self.parent(z), self.sibling(z)) # recur upward
    else: # Case 3: y is red; rotate misaligned 3-node and repeat
      self._rotate(y)
      self._set_black(y)
      self._set_red(z)
      if z == self.right(y):
        self._fix_deficit(z, self.left(z))
      else:
        self._fix_deficit(z, self.right(z))

Splay Trees

Splay trees are a type of self-adjusting binary search tree with the unique property that recently accessed elements are moved to the root of the tree using a process called splaying. This makes frequently accessed elements quicker to access again in the future.

Key Characteristics

Unlike traditional binary search trees, splay trees do not maintain strict balance. Instead, they perform a series of rotations (splays) to move an accessed node to the root. This adaptive strategy optimizes the tree's structure based on usage patterns, often providing better performance for sequences of non-random operations.

Splaying Operations

Splaying involves performing rotations on a node until it becomes the root of the tree. There are several types of splay operations, depending on the position of the node and its parents:

• Zig: A single rotation is used when the node is a direct child of the root.
• Zig-Zig: A double rotation is used when both the node and its parent are either left children or right children.
• Zig-Zag: A double rotation of different types (first right then left, or first left then right) is used when the node is a right child and its parent is a left child, or vice versa.

Insertion in Splay Trees

Insertion in a splay tree follows these steps:

1. Insert the new node: First, insert the new node using the standard binary search tree insertion procedure.
2. Splay the node: After insertion, splay the inserted node, moving it to the root of the tree.

Deletion in Splay Trees

Deletion in a splay tree involves:

1. Splay the node: First, splay the node to be deleted, bringing it to the root of the tree.
2. Remove the node: If the node has two children, replace it with its successor or predecessor, then splay that node to the root and remove the original node. If it has one or no children, simply remove it as in a BST.

Searching in Splay Trees

To search for a value in a splay tree:

1. Perform standard BST search: Find the node containing the value.
2. Splay the node: Whether found or not, splay the last accessed node to the root.

Performance of Splay Trees

The performance of splay trees is not strictly \(O(\log n)\) for individual operations. However, they offer amortized \(O(\log n)\) performance over a sequence of operations due to the self-adjusting nature of splaying. This makes them particularly effective for applications with non-uniform access patterns.

(2,4) Trees

(2,4) trees, also known as 2-4 trees, are a type of balanced tree data structure that provides an efficient way to manage and search for data. They are a special case of B-trees and are particularly useful in databases and filesystems.

Key Characteristics

• Node Capacity: Each node in a (2,4) tree can have between 2 and 4 children, and accordingly, 1 to 3 keys.
• Balanced Height: All leaves are at the same depth, which ensures that operations are performed in logarithmic time.
• Flexible Node Configuration: The ability to have a variable number of children and keys allows (2,4) trees to remain balanced with a minimal number of tree rotations and rebalancing.

Operations in (2,4) Trees

Insertion

When inserting a new key into a (2,4) tree: 1. Find the correct leaf node where the key should be inserted, following standard tree search procedures. 2. Insert the key into the node. - If the node has fewer than 3 keys, simply add the new key. - If the node already contains 3 keys, it is split into two nodes, each with fewer keys, and the middle key is moved up to the parent. This process may propagate up the tree.

Deletion

Deletion from a (2,4) tree involves: 1. Locating the key to be deleted. 2. Removing the key and rebalancing the tree. - If removing the key would leave a node with fewer than 1 key, keys or nodes are redistributed to maintain the tree's balance. This might involve borrowing a key from a sibling node or merging with a sibling if both have the minimum number of keys.

Searching

Searching for a key in a (2,4) tree follows the basic principles of binary search within the keys of each visited node and choosing the appropriate child to continue the search based on the comparison.

Balancing and Performance

• Balancing: (2,4) trees are self-balancing, with each operation ensuring that the tree remains balanced, thus maintaining its performance guarantees.
• Performance: The operations of search, insertion, and deletion in a (2,4) tree all have a worst-case time complexity of \(O(\log n)\), where \(n\) is the number of keys in the tree.

Segment Trees

TODO: Add notes here - leaving blank for now.

Fenwick Trees

TODO: Add notes here - leaving blank for now.

References

---

1. Skiena, Steven S.. (2008). The Algorithm Design Manual, 2^nd ed. (2). : Springer Publishing Company. ↩

2. Goodrich, M. T., Tamassia, R., & Goldwasser, M. H. (2013). Data Structures and Algorithms in Python (1^st ed.). Wiley Publishing. ↩

3. Cormen, T. H., Leiserson, C. E., & Rivest, R. L. (1990). Introduction to algorithms. Cambridge, Mass. : New York, MIT Press. ↩