Algorithmic Analysis
Key Metrics
- Time Complexity: Measures the time taken by an algorithm to execute as a function of input size.
- Space Complexity: Measures the amount of memory required by an algorithm as a function of input size.
- Scalability: Determines how an algorithm's performance scales with increasing input size.
Techniques
- Big O Notation (\(O\)): Provides an upper bound on the growth rate of an algorithm's resource usage.
- Big Omega Notation (\(\Omega\)): Provides a lower bound on the growth rate of an algorithm's resource usage.
- Big Theta Notation (\(\Theta\)): Provides tight bounds on the growth rate of an algorithm's resource usage.
Common Asymptotic Functions
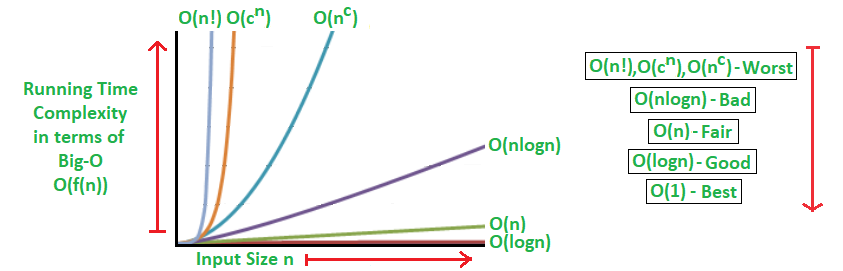
\(O(1)\) - Constant Time
- Represents algorithms with constant time complexity, independent of input size.
- Examples include accessing an element in an array or performing basic arithmetic operations.
\(O(\log n)\) - Logarithmic Time
- Represents algorithms whose time complexity grows logarithmically with the input size.
- Examples include binary search and certain tree operations like finding elements in balanced binary search trees.
\(O(n)\) - Linear Time
- Represents algorithms whose time complexity grows linearly with the input size.
- Examples include linear search, traversing an array, and simple array manipulations.
\(O(n \log n)\) - Linearithmic Time
- Represents algorithms whose time complexity grows log-linearly with the input size.
- Examples include efficient sorting algorithms like merge sort, heap sort, and quicksort.
\(O(n^2)\) - Quadratic Time
- Represents algorithms whose time complexity grows quadratically with the input size.
- Examples include bubble sort, selection sort, and certain matrix operations like matrix multiplication.
\(O(2^n)\) - Exponential Time
- Represents algorithms whose time complexity grows exponentially with the input size.
- Examples include certain recursive algorithms like generating all subsets of a set.
Notations
Big O Notation (\(O\))
- Represents the upper bound or worst-case scenario of an algorithm's time or space complexity.
- Example: \(O(n)\) denotes linear time complexity, indicating that the algorithm's runtime grows linearly with the input size.
Big Omega Notation (\(\Omega\))
- Represents the lower bound or best-case scenario of an algorithm's time or space complexity.
- Example: \(\Omega(1)\) denotes constant time complexity, indicating that the algorithm's runtime is constant regardless of input size.
Big Theta Notation (\(\Theta\))
- Represents tight bounds on an algorithm's time or space complexity, providing both upper and lower bounds.
- Example: \(\Theta(n^2)\) denotes quadratic time complexity, indicating that the algorithm's runtime grows quadratically with the input size.
