Skip to content

Linked Lists

There are some notable disadvantages of dynamic arrays like list in Python

  1. the length of the dynamic array might be longer than the actual number of elements it stores
  2. amortized bounds for operations may be unacceptable in real-time systems
  3. insertions and deletions at interior positions of an array are expensive

Linked lists provide an alternative to array-based ordered sequences.

While an array provides more centralized representation with one large chunk of memory capable of accommodating references to many elements, a linked list relies on a distributed representation using a lightweight object called a node for each element.

Each node maintains a reference to its element and one or more references to neighboring nodes in order to collectively represent the linear order of the sequence.

Trade-offs between Linked Lists and Arrays

Advantages of Array-Based Sequences

  1. Arrays provide O(1) time access to an element based on an integer index. Linked lists requires O(k) time to traverse the list from the beginning or possibly end of a doubly linked list.
  2. Operations with equivalent asymptotic bounds typically run a constant factor more efficiently with an array-based structure versus a linked structure. For example appending a new element to a linked list requires instantiation of a node, appropriate linking of nodes, and an increment of an integer. While this operation completes in O(1) time the actual number of CPU operations will be more in the linked version.
  3. Array based representations typically use proportionally less memory than linked structures. A dynamic array may be, in the worst case, allocated memory for 2n object references. With linked lists however the memory must be devoted not only to store a reference to each contained object, but also explicit references that link the nodes. So a singly linked list of length n already requires 2n references, and a doubly linked list 3n references.
  1. Link based structures provide worst-case time bounds for their operations. This is in contrast to amortized bounds associated with the expansion and contraction of a dynamic array. In real-time systems designed for more immediate responses, a long delay caused a single (amortized) operation may have an adverse effect. Worst-case bound gives a guarantee on the sum of the time spent on the individual operations.
  2. Link based structures support O(1) time insertions and deletions at arbitrary positions. This is perhaps the biggest advantage of linked lists.

Singly Linked List

A collection of nodes that collectively form a linear sequence. Each node stores a reference to an object that is an element of the sequence, as well as a reference to the next node of the list.

Each node is represented as a unique object, with that instance storing a reference to its element and a reference to the next node (or None). The linked list must keep a reference to the head of the list - without an explicit reference to the head, there would be no way to locate that node.

Unfortunately we cannot easily delete the last node of a singly linke list. The only way to access the node before the last is to start from the head of the list - which is inefficient. To make this efficient we will need a Doubly Linked List list.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class LinkedNode:
    __slots__ = '_element', '_next'

    def __init__(self, element, next):
        self._element = element
        self._next = next

class LinkedList:

    def __init__(self, head, tail):
        self._head = head
        self._tail = tail
        self._size = size

    def add_first(self, element):
        node = LinkedNode(element, self._head)
        self._head = node
        self._size += 1

    def add_last(self, element):
        node = LinkedNode(element, None)
        self._tail._next = node
        self._tail = node
        self._size += 1

    def remove_first(self):
        head = self._head
        self._head = self._head._next
        self._size -= 1

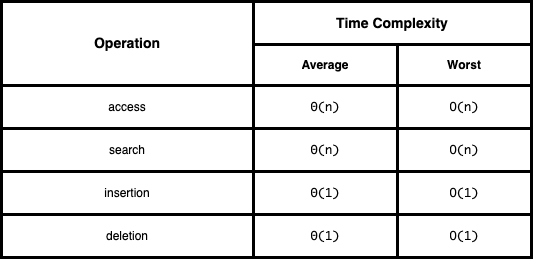
Efficiencies

Space Complexity: O(n)

Time Complexities:

Singly Linked List

Stack using a Singly Linked List

Using a singly linked list, we implement a stack. Since for a linked list we can insert and delete elements in constant time only at the head, we will use the head as the top of the stack.

When implementing the node we also intentionally define __slots__ to streamline the memory usage as there may potentially be many node instances in a single list.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Node:
    __slots__ = '_element', '_next'

    def __init__(self, element, next):
        self._element = element
        self._next = next


class LinkedStack:

    def __init__(self):
        self._head = None
        self._size = 0

    def __len__(self):
        return self._size

    def is_empty(self):
        return self._size == 0

    def push(self, e):
        self._head = Node(e, self._head)
        self._size += 1

    def top(self):
        if self.is_empty():
            raise Empty('Stack is Empty')
        return self._head._element

    def pop(self):
        if self.is_empty():
            raise Empty('Stack is Empty')

        answer = self._head._element

        self._head = self._head._next
        self._size -= 1
        return answer

Queue using a Singly Linked List

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Node:
    __slots__ = '_element', '_next'

    def __init__(self, element, next):
        self._element = element
        self._next = next


class LinkedQueue:

    def __init__(self):
        self._head = None
        self._tail = None
        self._size = 0

    def __len__(self):
        return self._size

    def is_empty(self):
        return self._size == 0

    def first(self):
        if self.is_empty():
            raise Empty('Queue is empty')
        return self._head._element

    def dequeue(self):
        if self.is_empty():
            raise Empty('Queue is empty')

        answer = self._head._element
        self._head = self._head._next
        self._size -= 1
        if self.is_empty():
            self._tail = None

        return answer

    def enqueue(self, element):
        newest = Node(element, None)
        if self.is_empty():
            self._head = newest
        else:
            self._tail._next = newest
        self._tail = newest
        self._size += 1

Circularly Linked Lists

Case where the next reference of the tail of the list circularly points back to the head of the list.

Example of use

A Round-Robin scheduler iterates through a collection of elements in a circular fashion and "services" each element by performing a given action on it. These are usually used to fairly allocate a resource that must be shared by a collection of clients e.g. to allocate slices of CPU time to various applications running concurrently on a computer.

Round robin queues can be implemented using a general queue with the following operations: 1. current_process = queue.dequeue() 2. Service current_process 3. queue.enqueue(current_process)

With a circular linked list implementation of a queue, we just have to incrementing a reference that marks the head and tail of the queue without needing to do any operations.

Circular Queue implemented

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Node:
    __slots__ = '_element', '_next'

    def __init__(self, element, next):
        self._element = element
        self._next = next


class LinkedQueue:

    def __init__(self):
        self._tail = None
        self._size = 0

    def __len__(self):
        return self._size

    def is_empty(self):
        return self._size == 0

    def first(self):
        if self.is_empty():
            raise Empty('Queue is empty')
        head = self._tail._next
        return head._element

    def dequeue(self):
        if self.is_empty():
            raise Empty('Queue is empty')
        oldhead = self._tail._next
        if self._size == 1:
            self._tail = None
        else:
            self._tail._next = oldhead._next
        self._size -= 1
        return oldhead._element

    def enqueue(self, element):
        newest = Node(element, None)
        if self.is_empty():
            newest._next = newest
        else:
            newest._next = self._tail._next
            self._tail._next = newest
        self._tail = newest
        self._size += 1

    def rotate(self):
        if self._size > 0:
            self._tail = self._tail._next

Doubly Linked List

Each node keeps an explicit reference to the node before it and a reference to the node after it. This is known as a doubly linked list. This allows for a greater variety of O(1) updates, inlcuding insertions and deletions at arbitrary positions within the list.

header and trailer sentinels - i.e. special "dummy" nodes - will be used as the head and tail of the list. By using just slightly extra space, our logic of operations greatly simplifies. 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Node:
    __slots__ = '_element', '_prev', '_next'

    def __init__(self, element, prev, next):
        self._element = element
        self._prev = prev
        self._next = next


class DoublyLinkedList:

    def __init__(self):
        self._header = Node(None, None, None)
        self._trailer = Node(None, None, None)
        self._header._next = self._trailer
        self._trailer._next = self._header
        self._size = 0

    def __len__(self):
        return self._size

    def is_empty(self):
        return self._size == 0

    def _insert_between(self, element, predecessor, successor):
        newest = Node(element, predecessor, successor)
        predecessor._next = newest
        successor._prev = newest

        self._size += 1
        return newest

    def _delete_node(self, node):
        pred = node._prev
        succ = node._next
        pred._next = succ
        succ._prev = pred
        self._size -= 1
        element = node._element
        node._prev = node._next = node._element = None
        return element

Implementing a Dequeue using a Doubly Linked List

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class LinkedDequeue(DoublyLinkedBase):

    def first(self):
        if self.is_empty():
            raise Empty('Dequeue is empty')

        return self._header._next._element

    def last(self):
        if self.is_empty():
            raise Empty('Dequeue is empty')
        return self._trailer._prev._element

    def insert_first(self, element):
        self._insert_between(element, self._header, self._header._next)

    def insert_last(self, element):
        self._insert_between(element, self._trailer._prev, self.trailer)

    def delete_first(self):
        if self.is_empty():
            raise Empty('Dequeue is empty')
        return self._delete_node(self._header._next)

    def delete_last(self):
        if self.is_empty():
            raise Empty('Dequeue is empty')
        return self._delete_node(self._trailer._prev)

References

  1. Skiena, Steven S.. (2008). The Algorithm Design Manual, 2nd ed. (2). : Springer Publishing Company. ↩

  2. Goodrich, M. T., Tamassia, R., & Goldwasser, M. H. (2013). Data Structures and Algorithms in Python (1st ed.). Wiley Publishing. ↩

  3. Cormen, T. H., Leiserson, C. E., & Rivest, R. L. (1990). Introduction to algorithms. Cambridge, Mass. : New York, MIT Press. ↩