Queues and Deques

Queues

A queue is a collection of objects that are inserted and removed according to the first-in, first-out (FIFO) principle. Elements can be inserted at any time, but only the elements that has been in the queue the longest can be next removed.

Some common methods supported by a queue are:

• queue.enqueue(e) - add an element e to the back of a queue
• queue.dequeue() - remove and return the first element from a stack
• queue.first() - return the first element of a stack
• queue.is_empty() - check if queue is empty
• len(queue) - the number of elements in a queue

Array-Based Queue Implementation

Utilizing a list for a queue would be very inefficient - this is because pop(0) i.e. a pop on a non-default index causes a loop to be executed that shifts all elements beyon the index to te left. This would cause the worst-case behavior of O(n) time.

Therefore we need to implement a queue using a circular array with the following logic:

1. initialize a list with a fixed size that is larger than the actual number of elements t be ever added tot he queue
2. define front as the index of the "first" element of a queue
3. enqueue items to the index calculated by (front + size) % capacity of the queue
4. for example for a queue of size 3, enqueue of [2, 1, 4] would be built as following: [2, None, None] -> [2, 1, None] -> [2, 1, 4]
5. then following dequeue operations will happen like so: [None, 1, 4] and front = 1 -> [None, None, 4] and front = 2 etc.
6. whenever the size of the queue is equal to its capacity, resize it to be double the capacity, and whenever the size is ¼th of the capacity, resize it to be half the capacity

class Empty(Exception):
    """Error attempting to access an element from an empty container."""
    pass

class ArrayQueue:
    """FIFO queue implementation using list"""

    DEFAULT_CAPACITY = 10

    def __init__(self):
        self._data = [None] * ArrayQueue.DEFAULT_CAPACITY
        self._size = 0
        self._front = 0

    def __len__(self):
        return self._size

    def is_empty(self):
        return self._size == 0

    def first(self):
        if self.is_empty():
            raise Empty('Queue is Empty')

        return self._data[self._front]

    def dequeue(self):
        if self._is_empty():
            raise Empty('Queue is Empty')

        answer = self._data[self._front]

        self._data[self._front] = None
        self._front = (self._front + 1) % len(self._data)
        self._size -= 1

        if 0 < self._size < len(self._data) // 4:
            self._resize(len(self._data) // 2)

        return answer

    def enqueue(self, e):
        if self._size == len(self._data):
            self._resize(2 * len(self.data))

        avail = (self._front + self._size) % len(self._data)
        self._data[avail] = e
        self._size += 1

    def _resize(self, cap):
        old = self._data
        self._data = [None] * cap
        walk = self._front

        for k in range(self._size):
            self._data[k] = old[walk]
            walk = (1 + walk) % len(old)

        self._front = 0

Efficiencies

Space Complexity: O(n)

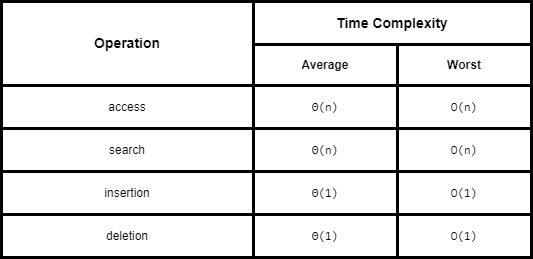
Time Complexities:

Dequeue - Double-Ended Queues

A queue like data structure that supports insertion and deletion from both the front and back of the queue.

An implementation of this is available through the deque class in Python in the standard collections module.

Array-Based Deqeue Implementation

We can implement a deque in a similar way as the Queue. The main modifications are:

1. adding a pointer to the last element as .last() where last = (self._front + self._size - 1) % len(self._data)
2. ability to add and remove from the back of the queue

class Empty(Exception):
    """Error attempting to access an element from an empty container."""
    pass

class ArrayQueue:
    """FIFO queue implementation using list"""

    DEFAULT_CAPACITY = 10

    def __init__(self):
        self._data = [None] * ArrayQueue.DEFAULT_CAPACITY
        self._size = 0
        self._front = 0

    def __len__(self):
        return self._size

    def is_empty(self):
        return self._size == 0

    def first(self):
        if self.is_empty():
            raise Empty('Queue is Empty')

        return self._data[self._front]

    def last(self):
        if self.is_empty():
            raise Empty('Queue is Empty')

        back = (self._front + self._size - 1) % len(self._data)

        return back

    def add_first(self, e):
        if self._size == len(self._data):
            self._resize(2 * len(self.data))

        self._front = (self._front - 1) % len(self._data)
        self._data[self._front] = e
        self._size += 1

    def delete_first(self):
        if self.is_empty():
            raise Empty('Deque is Empty')

        answer = self._data[self._front]

        self._data[self._front] = None
        self._front = (self._front + 1) % len(self._data)
        self._size -= 1

        if 0 < self._size < len(self._data) // 4:
            self._resize(len(self._data) // 2)

        return answer

    def add_last(self, e):
        if self._size == len(self._data):
            self._resize(2 * len(self.data))

        avail = (self._front + self._size) % len(self._data)
        self._data[avail] = e
        self._size += 1

    def delete_last(self):
        if self.is_empty():
            raise Empty('Deque is empty')

        back = self.last()
        answer = self._data[back]
        self._data[back] = None
        self._size -= 1

        if 0 < self._size < len(self._data) // 4:
            self._resize(len(self._data) // 2)

        return answer

    def _resize(self, cap):
        old = self._data
        self._data = [None] * cap
        walk = self._front

        for k in range(self._size):
            self._data[k] = old[walk]
            walk = (1 + walk) % len(old)

        self._front = 0

Efficiencies

Space Complexity: O(n)

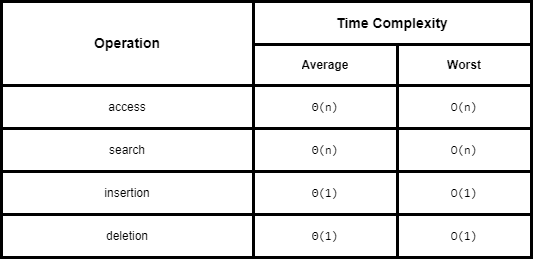
Time Complexities:

References

---

1. Skiena, Steven S.. (2008). The Algorithm Design Manual, 2^nd ed. (2). : Springer Publishing Company. ↩

2. Goodrich, M. T., Tamassia, R., & Goldwasser, M. H. (2013). Data Structures and Algorithms in Python (1^st ed.). Wiley Publishing. ↩

3. Cormen, T. H., Leiserson, C. E., & Rivest, R. L. (1990). Introduction to algorithms. Cambridge, Mass. : New York, MIT Press. ↩